Note
Go to the end to download the full example code.
Surrogate Models#
Some industrial applications require modeling complex processes that can result either in highly nonlinear functions or functions defined by a simulation process. In those contexts, optimization solvers often struggle. The reason may be that relaxations of the nonlinear functions are not good enough to make the solver prove an acceptable bound in a reasonable amount of time. Another issue may be that the solver is not able to represent the functions.
An approach that has been proposed in the literature is to approximate the problematic nonlinear functions via neural networks with ReLU activation and use MIP technology to solve the constructed approximation (see e.g. Heneao Maravelias 2011, Schweitdmann et.al. 2022). This use of neural networks can be motivated by their ability to provide a universal approximation (see e.g. Lu et.al. 2017). This use of ML models to replace complex processes is often referred to as surrogate models.
In the following example, we approximate a nonlinear function via
Scikit-learn MLPRegressor and then solve an optimization problem
that uses the approximation of the nonlinear function with Gurobi.
The purpose of this example is solely illustrative and doesn’t relate to any particular application.
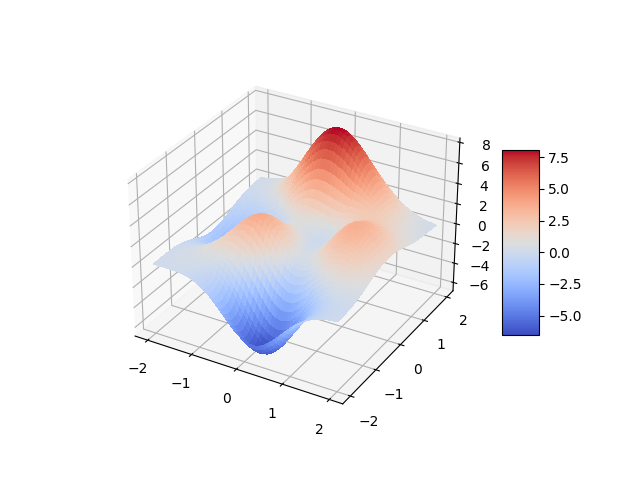
The function we approximate is the 2D peaks function.
The function is given as
In this example, we want to find the minimum of \(f\) over the interval \([-2, 2]^2\):
The global minimum of this problem can be found numerically to have value \(-6.55113\) at the point \((0.2283, -1.6256)\).
Here to find this minimum of \(f\), we approximate \(f(x)\) through a neural network function \(g(x)\) to obtain a MIP and solve
First import the necessary packages. Before applying the neural network,
we do a preprocessing to extract polynomial features of degree 2.
Hopefully this will help us to approximate the smooth function. Besides,
gurobipy, numpy and the appropriate sklearn objects, we also
use matplotlib to plot the function, and its approximation.
import gurobipy as gp
import numpy as np
from gurobipy import GRB
from matplotlib import cm
from matplotlib import pyplot as plt
from sklearn import metrics
from sklearn.neural_network import MLPRegressor
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from gurobi_ml import add_predictor_constr
Define the nonlinear function of interest#
We define the 2D peak function as a python function.
def peak2d(x1, x2):
return (
3 * (1 - x1) ** 2.0 * np.exp(-(x1**2) - (x2 + 1) ** 2)
- 10 * (x1 / 5 - x1**3 - x2**5) * np.exp(-(x1**2) - x2**2)
- 1 / 3 * np.exp(-((x1 + 1) ** 2) - x2**2)
)
To train the neural network, we make a uniform sample of the domain of
the function in the region of interest using numpy’s arrange
function.
We then plot the function with matplotlib.
x1, x2 = np.meshgrid(np.arange(-2, 2, 0.01), np.arange(-2, 2, 0.01))
y = peak2d(x1, x2)
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
# Plot the surface.
surf = ax.plot_surface(x1, x2, y, cmap=cm.coolwarm, linewidth=0.01, antialiased=False)
# Add a color bar which maps values to colors.
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
Approximate the function#
To fit a model, we need to reshape our data. We concatenate the values
of x1 and x2 in an array X and make y one dimensional.
X = np.concatenate([x1.ravel().reshape(-1, 1), x2.ravel().reshape(-1, 1)], axis=1)
y = y.ravel()
To approximate the function, we use a Pipeline with polynomial
features and a neural-network regressor. We do a relatively small
neural-network.
# Run our regression
layers = [30] * 2
regression = MLPRegressor(hidden_layer_sizes=layers, activation="relu")
pipe = make_pipeline(PolynomialFeatures(), regression)
pipe.fit(X=X, y=y)
To test the accuracy of the approximation, we take a random sample of points, and we print the \(R^2\) value and the maximal error.
X_test = np.random.random((100, 2)) * 4 - 2
r2_score = metrics.r2_score(peak2d(X_test[:, 0], X_test[:, 1]), pipe.predict(X_test))
max_error = metrics.max_error(peak2d(X_test[:, 0], X_test[:, 1]), pipe.predict(X_test))
print("R2 error {}, maximal error {}".format(r2_score, max_error))
R2 error 0.9998902991612034, maximal error 0.07220726535083566
While the \(R^2\) value is good, the maximal error is quite high. For the purpose of this example we still deem it acceptable. We plot the function.
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
# Plot the surface.
surf = ax.plot_surface(
x1,
x2,
pipe.predict(X).reshape(x1.shape),
cmap=cm.coolwarm,
linewidth=0.01,
antialiased=False,
)
# Add a color bar which maps values to colors.
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
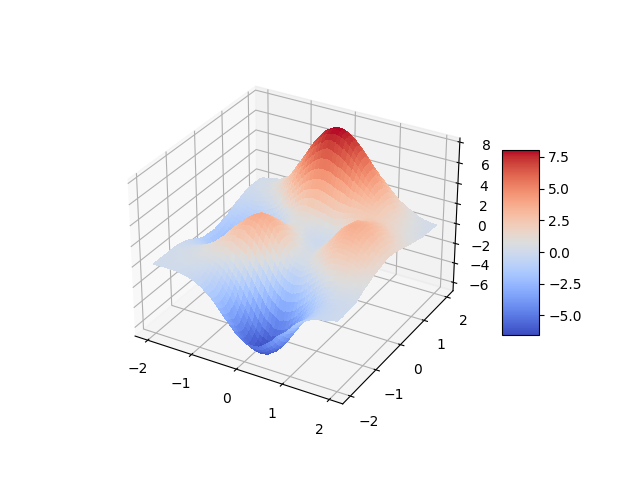
Visually, the approximation looks close enough to the original function.
Build and Solve the Optimization Model#
We now turn to the optimization model. For this model we want to find
the minimal value of y_approx which is the approximation given by
our pipeline on the interval.
Note that in this simple example, we don’t use matrix variables but regular Gurobi variables instead.
m = gp.Model()
x = m.addVars(2, lb=-2, ub=2, name="x")
y_approx = m.addVar(lb=-GRB.INFINITY, name="y")
m.setObjective(y_approx, gp.GRB.MINIMIZE)
# add "surrogate constraint"
pred_constr = add_predictor_constr(m, pipe, x, y_approx)
pred_constr.print_stats()
Restricted license - for non-production use only - expires 2025-11-24
Warning for adding constraints: zero or small (< 1e-13) coefficients, ignored
Model for pipe:
126 variables
61 constraints
6 quadratic constraints
60 general constraints
Input has shape (1, 2)
Output has shape (1, 1)
Pipeline has 2 steps:
--------------------------------------------------------------------------------
Step Output Shape Variables Constraints
Linear Quadratic General
================================================================================
poly_feat (1, 6) 6 0 6 0
dense (1, 30) 60 30 0 30 (relu)
dense0 (1, 30) 60 30 0 30 (relu)
dense1 (1, 1) 0 1 0 0
--------------------------------------------------------------------------------
Now call optimize. Since we use polynomial features the resulting
model is a non-convex quadratic problem. In Gurobi, we need to set the
parameter NonConvex to 2 to be able to solve it.
m.Params.TimeLimit = 20
m.Params.MIPGap = 0.1
m.Params.NonConvex = 2
m.optimize()
Set parameter TimeLimit to value 20
Set parameter MIPGap to value 0.1
Set parameter NonConvex to value 2
Gurobi Optimizer version 11.0.3 build v11.0.3rc0 (linux64 - "Ubuntu 20.04.6 LTS")
CPU model: Intel(R) Xeon(R) Platinum 8259CL CPU @ 2.50GHz, instruction set [SSE2|AVX|AVX2|AVX512]
Thread count: 1 physical cores, 2 logical processors, using up to 2 threads
Optimize a model with 61 rows, 129 columns and 991 nonzeros
Model fingerprint: 0x5ad72482
Model has 6 quadratic constraints
Model has 60 general constraints
Variable types: 129 continuous, 0 integer (0 binary)
Coefficient statistics:
Matrix range [3e-12, 1e+00]
QMatrix range [1e+00, 1e+00]
QLMatrix range [1e+00, 1e+00]
Objective range [1e+00, 1e+00]
Bounds range [2e+00, 2e+00]
RHS range [3e-03, 6e-01]
QRHS range [1e+00, 1e+00]
Presolve added 77 rows and 14 columns
Presolve time: 0.01s
Presolved: 148 rows, 143 columns, 1135 nonzeros
Presolved model has 3 bilinear constraint(s)
Solving non-convex MIQCP
Variable types: 101 continuous, 42 integer (42 binary)
Root relaxation: objective -5.677114e+01, 156 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 -56.77114 0 27 - -56.77114 - - 0s
0 0 -48.78035 0 33 - -48.78035 - - 0s
0 0 -48.77520 0 32 - -48.77520 - - 0s
0 0 -43.19988 0 31 - -43.19988 - - 0s
0 0 -40.90934 0 36 - -40.90934 - - 0s
0 0 -38.56541 0 36 - -38.56541 - - 0s
0 0 -37.49880 0 36 - -37.49880 - - 0s
0 0 -35.11500 0 36 - -35.11500 - - 0s
0 0 -35.11500 0 39 - -35.11500 - - 0s
0 0 -34.98799 0 38 - -34.98799 - - 0s
0 0 -34.98799 0 40 - -34.98799 - - 0s
0 0 -34.98799 0 40 - -34.98799 - - 0s
0 0 -34.98799 0 39 - -34.98799 - - 0s
0 0 -34.36503 0 41 - -34.36503 - - 0s
0 0 -34.36503 0 41 - -34.36503 - - 0s
0 0 -34.36503 0 41 - -34.36503 - - 0s
0 0 -34.36503 0 41 - -34.36503 - - 0s
0 0 -33.80457 0 39 - -33.80457 - - 0s
H 0 0 0.8804056 -33.80457 3940% - 0s
H 0 0 0.6590934 -33.80457 5229% - 0s
H 0 0 0.6590934 -33.80457 5229% - 0s
0 2 -33.11488 0 39 0.65909 -33.11488 5124% - 0s
H 54 43 -0.0438220 -32.83982 - 14.4 0s
* 445 199 37 -4.4858265 -23.06473 414% 12.4 0s
H 452 200 -4.4858281 -22.95401 412% 12.4 0s
* 502 189 37 -6.5610300 -22.95401 250% 11.7 0s
* 504 183 38 -6.5622795 -22.95401 250% 11.6 0s
* 506 181 39 -6.5622905 -22.95401 250% 11.6 0s
* 507 178 40 -6.5622910 -22.95401 250% 11.6 0s
* 508 177 40 -6.5622913 -22.95401 250% 11.5 0s
* 902 270 45 -6.5622915 -19.14066 192% 14.1 1s
H 1272 270 -6.5622916 -15.84065 141% 15.2 1s
H 1389 233 -6.5622917 -15.34230 134% 15.0 1s
Cutting planes:
Gomory: 7
Implied bound: 22
MIR: 51
Flow cover: 24
Relax-and-lift: 5
Explored 3229 nodes (48869 simplex iterations) in 2.76 seconds (1.95 work units)
Thread count was 2 (of 2 available processors)
Solution count 10: -6.56229 -6.56229 -6.56229 ... 0.880406
Optimal solution found (tolerance 1.00e-01)
Best objective -6.562291657001e+00, best bound -7.199277458505e+00, gap 9.7068%
After solving the model, we check the error in the estimate of the Gurobi solution.
print(
"Maximum error in approximating the regression {:.6}".format(
np.max(pred_constr.get_error())
)
)
Maximum error in approximating the regression 8.1549e-07
Finally, we look at the solution and the objective value found.
print(
f"solution point of the approximated problem ({x[0].X:.4}, {x[1].X:.4}), "
+ f"objective value {m.ObjVal}."
)
print(
f"Function value at the solution point {peak2d(x[0].X, x[1].X)} error {abs(peak2d(x[0].X, x[1].X) - m.ObjVal)}."
)
solution point of the approximated problem (0.1745, -1.676), objective value -6.562291657000748.
Function value at the solution point -6.49760990031769 error 0.06468175668305776.
The difference between the function and the approximation at the computed solution point is noticeable, but the point we found is reasonably close to the actual global minimum. Depending on the use case this might be deemed acceptable. Of course, training a larger network should result in a better approximation.
Copyright © 2023 Gurobi Optimization, LLC
Total running time of the script: (0 minutes 17.019 seconds)